|
|
|
\require{AMSmath}

Reageren...
Re: Re: Getallen
Hoe kan ik van de regel sin (a+b)= sin a·cos b+ cos a·sin b de formules sin(2a) en sin(a/2) afleiden. Alvast bedankt, roeten
Antwoord
Hoi,
Formule afleiden voor sin($\alpha$+$\beta$) = sin$\alpha$·cos$\beta$ + cos$\alpha$·sin$\beta$
Beschouw onderstaande rechthoek
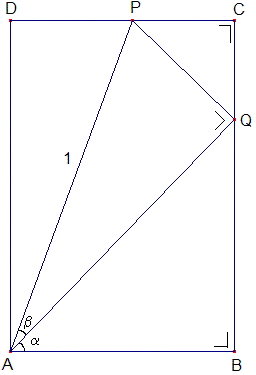
P en Q zijn zo gekozen dat $\angle$AQP = 90° en AP = 1.
$\angle$PQC = $\alpha$, want $\angle$BQA = 90° - $\alpha$ en $\angle$BQC = 180° (gestrekte hoek) $\Rightarrow$ $\angle$PQC = 180°-$\angle$BQA - $\angle$AQP = 180° - (90° - $\alpha$) - 90° = $\alpha$.
$\angle$APD = $\alpha$+$\beta$, dat zou je kunnen bewijzen a.d.h.v. een Z-hoek, want AB // DC $\Rightarrow$ $\angle$BAP = $\angle$DPA (je zou 't ook anders kunnen aanpakken: $\angle$ADP = 90°, $\angle$DAP = 90° - ($\alpha$+$\beta$) $\Rightarrow$ $\angle$ DPA = 180° - 90° - (90° - ($\alpha$+$\beta$)) = $\alpha$+$\beta$.
Nu gaan we 'n schema invullen (hou rekening met AP = 1)!

In de rechthoek geldt dat AD = BQ + QC. A.d.h.v. de tabel kunnen we laten zien dat sin($\alpha$+$\beta$) = AQ·sin$\alpha$+PQ·cos$\alpha$, want sin$\alpha$=BQ/AQ en cos$\alpha$=CQ/PQ en sin($\alpha$+$\beta$) = AD.
Invullen levert: AD = AQ·BQ/AQ + PQ·CQ/PQ $\Rightarrow$ AD = BQ + CQ.
We kunnen die AQ en PQ ook vervangen. Krijgen we sin($\alpha$+$\beta$) = cos$\beta$·sin$\alpha$ + sin$\beta$·cos$\alpha$ en aangezien bij de vermenigvuldiging de factoren van plaats mogen ruilen (want 4·3 = 3·4 bijvoorbeeld) mogen we ook schrijven sin($\alpha$+$\beta$) = sin$\alpha$·cos$\beta$+cos$\alpha$·sin$\beta$.
Om de regel van cos($\alpha$ + $\beta$) te bewijzen kun je gebruikmaken van het feit dat PD = AB - PC, en op analoge wijze krijg je dat cos($\alpha$+$\beta$) = cos$\alpha$·cos$\beta$ - sin$\alpha$·sin$\beta$ (we noemen deze formules de somformules)
Je kunt nu ook op de verschilformules hieruit afleiden, maar dan moet je wel weten dat cos(-t) = cos(t), sin(-t) = -sin(t).
Formule afleiden voor sin(2$\alpha$)
sin(2$\alpha$) = sin($\alpha$+$\alpha$). Dus gewoon $\beta$ vervangen door $\alpha$ in bovenstaande formule.
sin($\alpha$+$\alpha$) = sin$\alpha$·cos$\alpha$ + sin$\alpha$·cos$\alpha$ = 2sin$\alpha$·cos$\alpha$.
cos(2$\alpha$) gaat analoog, je krijgt cos2$\alpha$ - sin2$\alpha$ als uitkomst.
Formule afleiden van sin(1/2$\alpha$)
Vervang in bovenstaande formule $\alpha$ door 1/4$\alpha$.
sin(2·1/4$\alpha$) = 2sin(1/4$\alpha$)·cos(1/4$\alpha$)
Ik hoop dat het zo wat duidelijker is geworden, zo niet dan hoor ik het wel,
Groetjes,
Davy.
Gebruik dit formulier alleen om te reageren op de inhoud van de vraag en/of het
antwoord hierboven. Voor het stellen van nieuwe vragen kan je gebruik maken
van een vraag stellen in het menu aan de linker kant. Alvast bedankt!
|



